E望遠鏡の原理 光学の基礎
光学の基礎
概要 凸レンズや凹面反射鏡による対物鏡を使って、実物からの光を集めて実像を作り、それを接眼鏡によって虚像として拡大してみるというのが望遠鏡です。ここで、光を扱う光学の知識が幾分必要になります。そして、原理が判れば、製品の選択や使用に有利になると考えられます。
光学 光を使うものですから、光の性質を知ることが第一です。これが光学で、基本的な性質は次のようなものです。
1 光は 光は振動であり粒子である。
2 直進 光は真空中や、均一な媒質中を直進します。
3 反射 光は媒質の境界を通過する際に反射します。
4 屈折 光は媒質の境界を通過する際に屈折します。
1 光は、マクスウェルによって数式化された電磁場の周期的な変化が空間的に伝わっていく電磁波と呼ばれる横波の一部であって、光子と呼ばれる粒子としても捉えることができるものでもあり、エネルギーの伝達現象です。
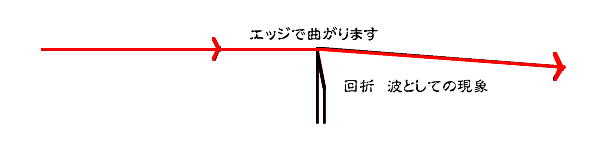
光を物理的に記述するには波としての波長を使い、?(ナノメートル)や、Å(オングストロームで表します。)波であることは回折や干渉が起こることから証明できますし、粒子としての性質は微小ながら光圧が存在していることから判っています。

2 直進 媒質(物理的作用を1つの場所から別の場所に伝達する仲介物)が、均一の場合や真空中では、光は直進します。そのときの速さは、媒質の性質と波長が関係しますが、媒質が無い状態(真空中)でも光は伝わり、そのときが最も速くなり、毎秒30万㎞となります。
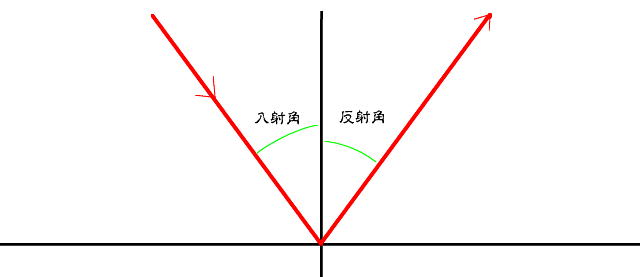
3 反射 媒質と別の媒質、または媒質と真空の境界を通過しようとするとき、光は反射します。境界面に入射した光が全て反射してしまうのが全反射です。入射の方向にある法線(境界面に対して垂直な方向線)から計った入射の角度と、反射した光が持つ反射角は等しくなります。これは媒質や境界での変化の状況や性質に寄らずに等しくなります。また、この現象は光の振動数にも影響されません。
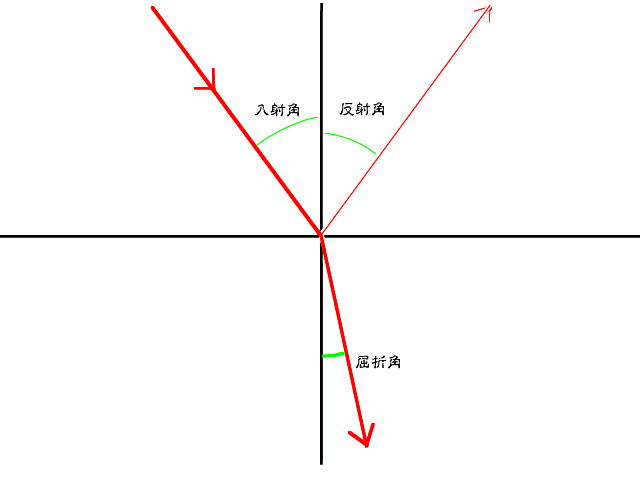
4 屈折 反射と同じ状況、媒質と別の媒質、または媒質と真空の境界を通過するときに、光の速度が変わることから、光の進行方向が変化します。入射の方向にある法線から計った入射の角度(入射角)と、反対方向の法線と曲がった進行方向との角度(屈折角)の比率は、境界面の両側の媒質または真空の性質によって、一定の関係となります。この比率は光の波長によっても変化します。これを色分散と呼びます。
色とは

光の波長の長い方から、赤橙黄緑青藍紫の七色が可視光の範囲として連続的に変わります。この色(光)を混ぜることで、全ての色を表現することができます。また、目には見えない光があり、紫外線・赤外線と呼ばれています。この色の見え方は個人差があります。

波長と色の関係はほぼ決まっていますが、連続的なものなので、色から波長を特定するのはなかなか難しいことです。しかし、太陽の光をプリズムで分解すると、その中に暗線が発見されました。フラウンフォーファー線と名付けられましたが、太陽大気の性質から吸収された波長で、これを基準にして屈折率の波長による変化などを調べることができるようになりました。現在でもc線やD線、f線等と呼ばれる波長について、対物レンズの特性をグラフ化して性能を示すことが行われています。
人間の目では目の網膜にある錐体細胞(色を感じる細胞)は、赤、緑、青のそれぞれを感じ取る3種があり、3つのセットで色を感じるようになっています。この原理を使い、ディスプレイでは、この三色を用いて色を表現しています。3色を合わせると白色になります。
発光体からの色は、光の三原色によって再構成できますが、通常の色は、発光体からの光を反射することによって生じています。ですから、赤い紙は、白い光(全ての色が含まれている光)が当たったときに、赤い光だけを反射しているのです。ですから、赤以外の光で照らせば、赤い紙は赤く見えずに、黒く見えることになります。この場合の色の付け方は、色の三原色を用いることになります。マゼンタ・シアン・イエローの三色を使い、3色を合わせると黒になります。色素の問題で、3色を合わせて純黒にはなかなかならないので、プリンターでは、黒を別に用意し、更に色表現を精密に行うために多色のインクを使用しているものがあります。
光学の初歩
反射や屈折の法則から、実体の位置の見え方が変わることの理屈が付きます。
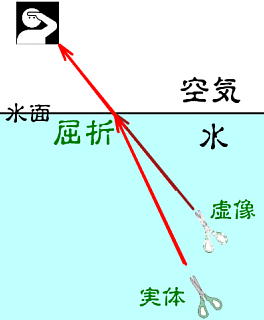
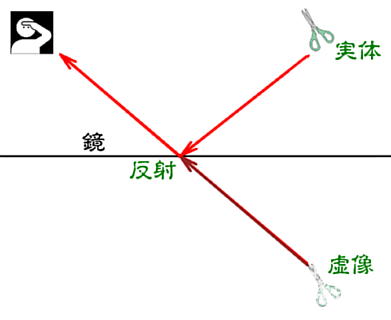
水面で光が屈折することにより、中にあるものが浮き上がって見えます。この場合、距離が違って見えますし、浮き上がって見える分、上下方向に圧縮されて見えます。これは媒質の中を通るときの光の速度が変わるためで、これが光が曲がる原因となります。鏡では、光が反射することから、実際には無い場所に物が見えます。物体の大きさは変わりませんが、裏返しに見えます。実際には実体が無いところに見えますから、それを像と呼びます。そして、像のところに実際には光が集まっているわけではなく、そう見えるだけなので虚像と呼びます。
レンズ
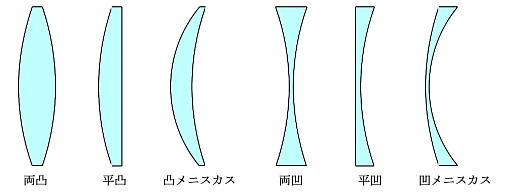
球状の面を持つ透明な材料を使った光学素子をレンズと呼びます。レンズには凸レンズと凹レンズがあり、縁が薄く中が盛り上がっているのが凸レンズです。これに対し、縁が厚くなっていて中が薄くなっているのが凹レンズです。形により、両凸レンズ、平凸レンズ、凸メカニクス、両凹レンズ、平凹レンズ、凹メカニクスというように名前がついています。断面図を示しましょう。
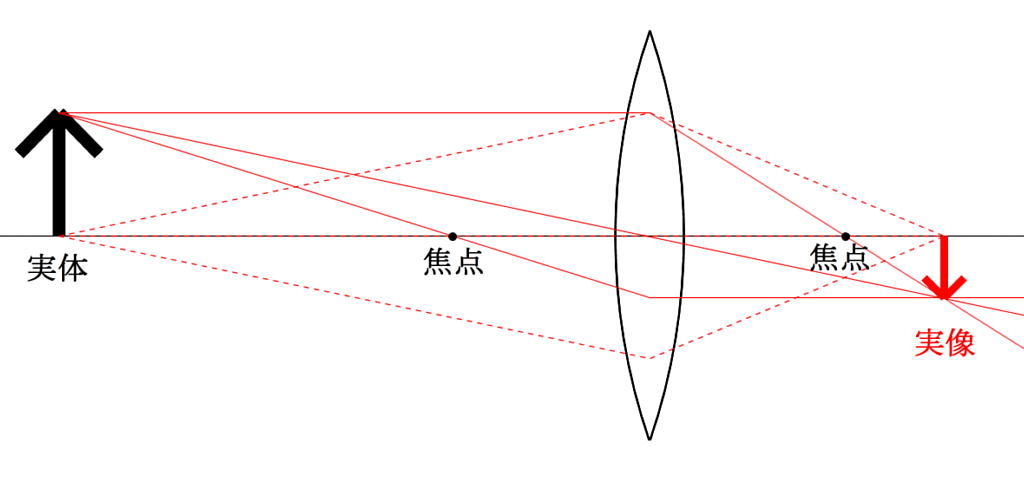
凸レンズは光を集めます。太陽光線のような平行光線を凸レンズに通すと、一点に集まるように見えます。この集まった点を焦点と呼びます。レンズの中心から、焦点までの距離を焦点距離と呼びます。遠いところからの光は焦点のある面に実像を作ります。これがカメラの原理であり、眼もこれを利用しています。実体がレンズに近づくに従って像は焦点から外側に移動していきます。物体を焦点に置くと、原理的にはレンズを通過した光は平行光線となり、像を結ばないようになります。
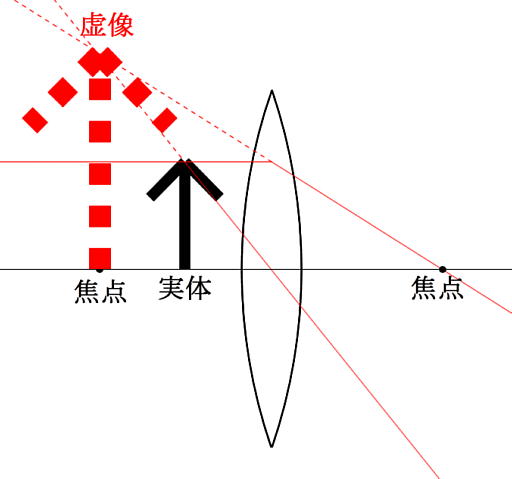
更に実体をレンズに近付けると、レンズの反対側から見てそこに物体があるかのような像、虚像を作るようになります。これが虫眼鏡の原理です。
③収差対策
これらの収差をどのように解消するかが光学設計上の腕の見せ所であり、実際の製品製造の技術精度も考える必要のある困難な分野でもあります。現在では非球面の製造が昔に比べて量産できるようになったり、特殊な性質を持つガラス材を作ることが出来るようになっているので、新しい製品は昔に比べて格段に高い性能を持つようになってきています。
(2)焦点距離
凹面反射鏡や両凸レンズ(単体)では、焦点距離を測るのはそれ程難しくありません。しかし、何枚ものレンズを組み合わせて厚くなった光学系では、どこを基準にしたら良いのかが判らなくなります。この為、レンズ系の対物側を前として、レンズ系の前後を区別し、前または後ろから入った光がどこで焦点となるのかを問題にします。前側から入った平行光線がレンズ系を通過して後ろ側の一点に集まるのですが、焦点に集まる光を1枚の曲面(後側主要面、主面)で集めたと考えて光路を作ります。この曲面と光軸の交点を主点(後側主点)と呼びます。ここから焦点までの距離を後側焦点距離とします。望遠鏡では一般に後側焦点距離が問題となります。後ろから入った光についての焦点距離は前側焦点距離であり、その主点は前側主点になります。主点位置も焦点距離も前後で違うことが当たり前です。
(3)有効口径
主鏡に入った光が全て焦点に集まっていれば、主鏡の直径が口径になります。しかし、絞りやその他の理由で焦点に集まる光が絞られている場合は、実際に使われている口径を有効口径として表示します。カメラ用レンズでは周辺光量を確保するために前玉を大きくしていることが多く、前玉の直径を測って口径とすることが出来ません。このような場合はF数から有効口径を考えます。
(5)倍率
望遠鏡では主鏡の主焦点距離を接眼鏡の焦点距離で割ったものを倍率としています。カタログには付属させた接眼鏡との組み合わせで、この方法で計算された数値が載っていますが、実際には見る人の目との合成光学系として考える必要がありますし、近距離の場合は主焦点距離が伸びるので、倍率の数値は変わってきます。
目のピント位置は固定ではなく、正常視力であれば無限遠から10cm程度まで変えることが出来ます。一般に明視距離と呼ばれる25cmを基準として固定した場合、凹レンズを組み合わせて無限遠に焦点を合わせた遠視状態から、凸レンズを組み合わせて近場に焦点を合わせた近視状態まで変化できるということになります。更に、近視の人は凸レンズの度数が大きくななるのと同じで、ピントの合う距離が近づくのです。遠視の場合も凹レンズの度数がより大きくなり、焦点距離としてはマイナスの数値になります。
このように場合に、どこに目のピントがあるかによって、接眼鏡との合成焦点距離が変わり、望遠鏡の倍率が変わってきます。正常視力でもピント位置を寄せると倍率が上がるのです。この他に、接眼鏡と目の距離も合成光学系としては影響する数値です。
また、目のピントは可変であるのですが、見やすい距離というのもあります。明視距離がそれに当たりますが、主焦点の像をこの距離から見ると接眼鏡無しでも望遠鏡の像を見ることができます。この場合の倍率は接眼鏡(つまり眼)の焦点距離が250mmですから、倍率は主焦点距離を250mmで割ってやればよいことになります。また、目のピントの合っている距離を変えると、倍率も変えることができます。
次に無限遠からの平行光線は焦点に集まりますが、それより近いところからの光は、焦点よりも後に結像します。カメラレンズで一般的なものは近くにピントを合わせるために繰り出すようになっています。特にマクロレンズでは繰り出す量が大きくなります。これは近くを撮るために撮影焦点距離が伸びているのです。近いところからの場合、主焦点が伸びているのと同じになりますので、倍率は大きくなります。
製作上の問題で焦点距離が公称値ではない場合があります。特に単焦点の接眼鏡の場合は、誤差の大きいものが含まれていて、倍率の値が予期したものでない事がありがちです。これらを確認するには、本来は専用の瞳径測定装置を使うのですが、望遠鏡を明るいところに出し、接眼鏡を付けてやや離れたところから、接眼鏡の眼レンズを見ます。すると対物レンズから入った光が丸く見えます。これを射出瞳と呼びます。この光は高倍率になるほど小さく見えます。この直径をマイクロメーターやノギスなどでなるべく正確に測ります。百分の一ミリ程度の精度が本当は必要です。次に対物鏡の有効口径も確認します。有効口径を接眼側の光の大きさで割った数値が、望遠鏡の倍率です。主焦点距離はカタログ値よりそれ程違っていないはずですから、主焦点距離を倍率で割った値が接眼鏡の焦点距離になります。
この射出瞳、及びその直径(通称瞳径)は大きな意味を持ちます。
射出瞳をよく観察します。ルーペを使ってみることも出来ます。反射式では副鏡やその支持金具によるケラレが一目瞭然です。正立系を持つ光学系、特にプリズムを使うものでは、周囲が四角くケラレたり、弓形の光条が射出瞳外に出ますので、不具合がすぐ判ります。
この瞳径が眼の瞳の大きさを超えて大きい場合は、主鏡の光を目に全て入れることが出来ない状態です。口径を無駄にしているわけです。しかし、眼の瞳の大きさは周囲の明るさによって変わりますので、望遠鏡をどの状態で使うかということから設計する必要があります。一般に明るいところでは2mm、夕方や朝方の暗さでは5mm、月のない暗夜では7mmと言われています。天体望遠鏡ではこの7mmを使って、瞳径が7mmになる倍率を最低倍率としています。口径をmmで表して7で割った値ですが、簡単に概算するには口径をcmで表し、1.5倍(本当は1.4倍)することで最低倍率を求めることが出来ます。
瞳径が1mmよりも小さくなってくると、だんだんと眼球内のガラス体の歪みや浮遊物が目立つようになってきます。そこで瞳径が1mmになる倍率をその望遠鏡の実用最高倍率とします。口径をmmで表した数値の倍率になります。この倍率は、奇しくも分解能による最高倍率と一致する倍率が上限倍率となります。
これ以上の倍率を過剰倍率とします。瞳径が0.5mmよりも小さくなると飛蚊症のような状態になる人もいます。高倍率をかけすぎると返って見えにくくなるということです。ただし、過剰倍率は禁止ということではなく、分解能のところで説明したように対象と条件によっては、その方が見やすいためにしばしば使うものです。
光の回折現象に原因した望遠鏡の細かいところを見る能力の限界を分解能と呼びます。これは口径に比例又は逆比例する数値となります。最も使われているのはドーズによる実験式で115.8を口径ミリ数で割った値が使われ、角度の秒で表されます。口径100mmの望遠鏡の分解能は角度で1.158秒となります。現実には、設計上の収差や製作上の不良、使用上の不備、気象条件、体調等によって悪くなるものですから、上限の値なのですが、カタログ等には口径からの計算値が書かれています。
眼の分解能は、正常眼で視力1.2の人が角度で50秒といわれています。視力が1.0の人は60秒、視力2.0の人は30秒ということになります。しかし、眼自体が持つ能力としての分解能は網膜の細かさとそれを判断する脳細胞の経験値であって、視力が低い場合でも、多くの人は眼鏡で矯正することができます。矯正された視力が元になるので、近視や遠視、乱視は分解能には関係がありません。
望遠鏡の分解能を発揮させるには、この眼の分解能と望遠鏡の分解能を一致させる倍率が必要となります。正常眼の分解能である角度で50秒に対して、ドーズによる実験式を割り算すれば、その倍率が算出できます。概略で口径のミリ数の半分くらいになります。しかし、健康状態や眼の使用状況では視力が格段に落ちていることもありますから、視力としての分解能を落とし余裕を見て角度の120秒として考えると、概算では口径mm程度の倍率が必要となります。これが有効最大倍率となります。これ以上、倍率をかけると像が薄く、ぼやけてくるだけです。しかし、これは理論値ですから、重星のような限界近くを試すような場合は、見やすくするために、更に倍率をかける場合もありますが、常用するものではありません。
目で見る場合の分解能は倍率と関わりましたが、写真撮影を考えると、主焦点の像がどれだけ小さなものを区別できるか、どこまで分解するかを示すという方法もあります。この場合、像の位置での必要最小解像度が問題になります。この場合はカメラのレンズのようにフィルムやCCD等の最小単位の大きさから、どれだけの性能がレンズにあればよいかを逆算することができます。フィルムは30μmが一般的な粒子径であり、デジカメでは2μmというレベルのものから10μm位まであります。フィルムに合わせて設計されたレンズをデジタルに使うと、思うような性能が出ないことが多々ありますが、その原因はここにあります。レンズの設計上、そこまでの収差補正をしていないのです。また、カメラ用の望遠レンズを眼視用に転用してもあまり良い性能を出さない理由もここにあります。
一般に光学的能力で眼視に耐えるものであるならば、直焦点撮影には充分使えます。更に拡大して使えるのは間違いありません。逆に言えば、かなり見目が悪くても撮影には使えることがほとんどだということです。
望遠鏡の能力として、どれだけ光を集めることができるかという数値を表示する場合があります。倍率で説明したように眼を口径7mmの基本望遠鏡とした場合に、その何倍の光を集めるかという数値です。しかし、カタログに載っているのは、計算上の口径の面積比です。本来は光学系の反射や吸収、蹴られによって計算値から落ちますから、それを表示する為のものです。また、倍率と混同して表示する場合も未だに見かけます。
天体望遠鏡の場合、どれだけ暗い星が見えるかを表すためにこの数値を示す場合があります。しかし、これも口径から計算された数値です。星の明るさは、等級で表します。特に明るい星を1等星、見えるギリギリの暗い星を6等星として始まりましたが、1等星と6等星が100倍の明るさが違うという等比級数的関係が見いだされて、明るい方へも暗い方へも拡張されました。現在は肉眼用だけでなく写真や光電管などのための等級も用意されています。肉眼の等級は実視等級と呼びます。
以下の表は、瞳径7mmのヒトが6.0等級の星を見ることができるとした場合に、式 m=5log(口径/7)+1.774 で計算したものです。これは、口径7mm、焦点距離18mmの望遠鏡で見ることのできる星の等級という計算になります。実際には瞳径7mmのヒトが見ることのできる限界の等級は、空の状態や、体調や能力により変わってきます。多くのヒトが理想的や暗夜で充分に目を慣らすと6.5等級を見ることができるようです。
また、機材の光学的性能により星像が乱れている場合も、限界等級は容易に明るくなってしまいます。
| 口径cm | 集光力 | 眼視限界等級 | 分解能 |
| cm | 倍 | 等 | 秒角 |
| 0.5 | 0.51 | 5.3 | 23.2 |
| 0.7 | 1 | 6.0 | 16.5 |
| 1.5 | 5 | 7.7 | 7.7 |
| 2 | 8 | 8.3 | 5.8 |
| 2.5 | 13 | 8.8 | 4.6 |
| 3 | 18 | 9.2 | 3.9 |
| 4 | 33 | 9.8 | 2.9 |
| 5 | 51 | 10.3 | 2.3 |
| 6 | 73 | 10.7 | 1.9 |
| 7 | 100 | 11.0 | 1.7 |
| 8 | 131 | 11.3 | 1.4 |
| 9 | 165 | 11.5 | 1.3 |
| 10 | 204 | 11.8 | 1.2 |
| 11 | 247 | 12.0 | 1.1 |
| 12 | 294 | 12.2 | 1.0 |
| 13 | 345 | 12.3 | 0.9 |
| 15 | 459 | 12.7 | 0.8 |
| 18 | 661 | 13.1 | 0.6 |
| 20 | 816 | 13.3 | 0.6 |
| 25 | 1276 | 13.8 | 0.5 |
| 30 | 1837 | 14.2 | 0.4 |
| 35 | 2500 | 14.5 | 0.3 |
| 40 | 3265 | 14.8 | 0.3 |
| 45 | 4133 | 15.0 | 0.3 |
| 50 | 5102 | 15.3 | 0.2 |
| 60 | 7347 | 15.7 | 0.2 |
| 80 | 13061 | 16.3 | 0.1 |
| 100 | 20408 | 16.8 | 0.1 |
| 口径 cm |
眼視限界等級 |
| 0.5 | 5.3 |
| 0.7 | 6.0 |
| 1.5 | 7.7 |
| 2 | 8.3 |
| 2.5 | 8.8 |
| 3 | 9.2 |
| 4 | 9.8 |
| 5 | 10.3 |
| 6 | 10.7 |
| 7 | 11.0 |
| 8 | 11.3 |
| 9 | 11.5 |
| 10 | 11.8 |
| 11 | 12.0 |
| 12 | 12.2 |
| 13 | 12.3 |
| 15 | 12.7 |
| 18 | 13.1 |
| 20 | 13.3 |
| 25 | 13.8 |
| 30 | 14.2 |
| 35 | 14.5 |
| 40 | 14.8 |
| 45 | 15.0 |
| 50 | 15.3 |
| 60 | 15.7 |
| 80 | 16.3 |
| 100 | 16.8 |
撮影限界等級
肉眼に対してカメラは、光を貯めることができるので、上記の眼視限界等級よりも暗い星を写すことができます。しかし、夜空には夜光や黄道光、そして地上の照明によって、ある程度の明るさがあり、ある等級以上はカブリが生じて写せない限界があります。これは、撮影用の光学系によって星の像が何処まで収れんするのか、光学系の焦点距離、光の波長、背景の夜空の明るさなどが関係しています。実験式として 撮影限界等級=22+log(焦点距離)-2.5log(2.44*光の波長*口径比)-23.1
というものがあります。(2.44*光の波長*口径比)というのは、理想的な光学系で星像が収れんする大きさ、エアリーディスクの直径です。ただし、0.005mm以下の場合は0.005mmとして計算しています。2013年での高画素デジタル一眼の画素に合わせています。この式の計算結果は、前出の実視限界等級の28倍程度の能力になっています。
眼視限界等級と同じように、夜空の明るさや機材の状況によって限界等級は容易に下がってきます。
| 焦点距離f.l.と口径比Fによる撮影限界等級 | ||||||||||
| fl mm\F | 1.4 | 2 | 2.8 | 4 | 5.6 | 8 | 11 | 16 | 22 | 32 |
| 18 | 11.1 | 11.1 | 11.1 | 10.9 | 10.5 | 10.2 | 9.8 | 9.4 | 9.1 | 8.6 |
| 20 | 11.3 | 11.3 | 11.3 | 11.1 | 10.8 | 10.4 | 10.0 | 9.6 | 9.3 | 8.9 |
| 24 | 11.7 | 11.7 | 11.7 | 11.5 | 11.2 | 10.8 | 10.4 | 10.0 | 9.7 | 9.3 |
| 28 | 12.0 | 12.0 | 12.0 | 11.9 | 11.5 | 11.1 | 10.8 | 10.4 | 10.0 | 9.6 |
| 35 | 12.5 | 12.5 | 12.5 | 12.4 | 12.0 | 11.6 | 11.3 | 10.9 | 10.5 | 10.1 |
| 50 | 13.3 | 13.3 | 13.3 | 13.2 | 12.8 | 12.4 | 12.1 | 11.7 | 11.3 | 10.9 |
| 60 | 13.7 | 13.7 | 13.7 | 13.6 | 13.2 | 12.8 | 12.5 | 12.1 | 11.7 | 11.3 |
| 70 | 14.1 | 14.1 | 14.1 | 13.9 | 13.5 | 13.2 | 12.8 | 12.4 | 12.1 | 11.7 |
| 85 | 14.5 | 14.5 | 14.5 | 14.3 | 14.0 | 13.6 | 13.2 | 12.8 | 12.5 | 12.1 |
| 105 | 15.0 | 15.0 | 15.0 | 14.8 | 14.4 | 14.1 | 13.7 | 13.3 | 13.0 | 12.6 |
| 135 | 15.5 | 15.5 | 15.5 | 15.4 | 15.0 | 14.6 | 14.3 | 13.9 | 13.5 | 13.1 |
| 150 | 15.8 | 15.8 | 15.8 | 15.6 | 15.2 | 14.8 | 14.5 | 14.1 | 13.8 | 13.3 |
| 200 | 16.4 | 16.4 | 16.4 | 16.2 | 15.9 | 15.5 | 15.1 | 14.7 | 14.4 | 14.0 |
| 300 | 17.3 | 17.3 | 17.3 | 17.1 | 16.8 | 16.4 | 16.0 | 15.6 | 15.3 | 14.9 |
| 400 | 17.9 | 17.9 | 17.9 | 17.8 | 17.4 | 17.0 | 16.7 | 16.3 | 15.9 | 15.5 |
| 500 | 18.4 | 18.4 | 18.4 | 18.3 | 17.9 | 17.5 | 17.2 | 16.8 | 16.4 | 16.0 |
| 600 | 18.8 | 18.8 | 18.8 | 18.7 | 18.3 | 17.9 | 17.6 | 17.2 | 16.8 | 16.4 |
| 800 | 19.5 | 19.5 | 19.5 | 19.3 | 18.9 | 18.6 | 18.2 | 17.8 | 17.5 | 17.1 |
| 900 | 19.7 | 19.7 | 19.7 | 19.6 | 19.2 | 18.8 | 18.5 | 18.1 | 17.7 | 17.3 |
| 1000 | 20.0 | 20.0 | 20.0 | 19.8 | 19.4 | 19.1 | 18.7 | 18.3 | 18.0 | 17.5 |
| 1200 | 20.4 | 20.4 | 20.4 | 20.2 | 19.8 | 19.5 | 19.1 | 18.7 | 18.4 | 17.9 |
| 1800 | 21.3 | 21.3 | 21.3 | 21.1 | 20.7 | 20.4 | 20.0 | 19.6 | 19.3 | 18.8 |
| 2000 | 21.5 | 21.5 | 21.5 | 21.3 | 21.0 | 20.6 | 20.2 | 19.8 | 19.5 | 19.1 |
| 限界露出時間(追尾撮影(ガイド撮影)) | ||||||||
| F | ISO50 | ISO100 | ISO200 | ISO400 | ISO800 | ISO1600 | ISO3200 | ISO6400 |
| 1.4 | 32分 | 16分 | 8分 | 4分 | 2分 | 1分 | 30秒 | 15秒 |
| 2 | 1時間4分 | 32分 | 16分 | 8分 | 4分 | 2分 | 1分 | 30秒 |
| 2.8 | 2時間8分 | 1時間4分 | 32分 | 16分 | 8分 | 4分 | 2分 | 1分 |
| 4 | 4時間16分 | 2時間8分 | 1時間4分 | 32分 | 16分 | 8分 | 4分 | 2分 |
| 5.6 | 8時間32分 | 4時間16分 | 2時間8分 | 1時間4分 | 32分 | 16分 | 8分 | 4分 |
| 8 | 17時間4分 | 8時間32分 | 4時間16分 | 2時間8分 | 1時間4分 | 32分 | 16分 | 8分 |
| 11 | 34時間8分 | 17時間4分 | 8時間32分 | 4時間16分 | 2時間8分 | 1時間4分 | 32分 | 16分 |
| 16 | 34時間8分 | 17時間4分 | 8時間32分 | 4時間16分 | 2時間8分 | 1時間4分 | 32分 | |
| 32 | 34時間8分 | 17時間4分 | 8時間32分 | 4時間16分 | 2時間8分 | 1時間4分 | ||